2025年高职单招每日一练《数学(中职)》4月30日专为备考2025年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
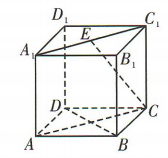
1、在正方体 ABCD-A1B1C1D1中,E为A1C1的中点,则异面直线 CE与 BD 所成的角为()
- A:30°
- B:45°
- C:60°
- D:90°
答 案:D
解 析:如图,连接 AC,则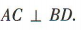 因为
因为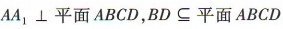 ,所以
,所以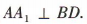 因为
因为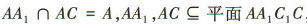 ,所以
,所以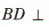 平面 AA1C1C.因为
平面 AA1C1C.因为 所以
所以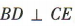 ,所以异面直线 CE 与 BD 所成的角为 90°.
,所以异面直线 CE 与 BD 所成的角为 90°.
2、已知向量a=(-1,1),b=(1,5),则2a+b=()
- A:(-3,6)
- B:(-1,7)
- C:(-1,-3)
- D:(-2,10)
答 案:B
解 析:因为向量a=(-1,1),b=(1,5),所以2a+b=2(-1,1)+(1,5)=(-1,7)
3、不等式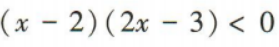 的解集是()
的解集是()
- A:
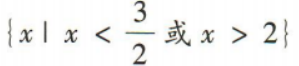
- B:R
- C:
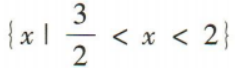
- D:∅
答 案:C
解 析:

主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、已知△ABC为等边三角形,则 的夹角为()
的夹角为()
答 案:120°
解 析:
2、若2a=3,b=log34,则ab=()
答 案:2
解 析: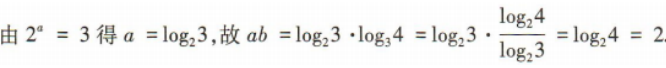
3、设等差数列{an}的公差d≠0,a1=4d,若ak是a1与a2k的等比中项,则k()
答 案:3
解 析: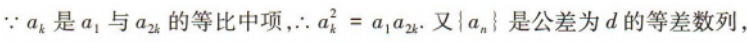
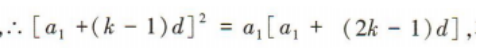

简答题
1、已知椭圆的两个焦点分别是 ,且椭圆与x轴的一个交点 A(-3,0).(1)求椭圆的标准方程;
,且椭圆与x轴的一个交点 A(-3,0).(1)求椭圆的标准方程;
(2)设P是椭圆上的任意一点,求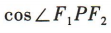 的最小值,
的最小值,
答 案:(1)设椭圆的标准方程为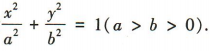 由题意得
由题意得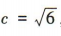 ,a=3,b2=a2-c2=3.
∴椭圆的标准方程为
,a=3,b2=a2-c2=3.
∴椭圆的标准方程为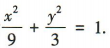 (2)由椭圆的定义及点P是椭圆上一点得|F1P|+|F2P|=2a=6,
由椭圆的两个焦点分别是
(2)由椭圆的定义及点P是椭圆上一点得|F1P|+|F2P|=2a=6,
由椭圆的两个焦点分别是 ,得
,得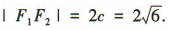 设|F1P|=m(0
设|F1P|=m(0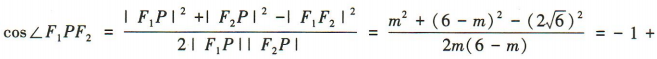
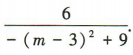 当m=3时,
当m=3时,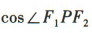 取得最小值,最小值为
取得最小值,最小值为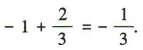
精彩评论