2025年成考高起点每日一练《数学(理)》2月12日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、抛物线y＝ax²（a＜0）的焦点坐标是（）。

• A：
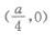
• B：
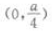
• C：
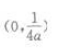
• D：

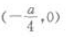
答 案：C

解 析：

2、设函数f(x)＝e^x，则f(x－a)·f(x＋a)＝（）。

• A：f(x²－a²)
• B：2f(x)
• C：f(x²)
• D：f²(x)

答 案：D

3、函数y=-x²+2x的值域是（）。  

• A：[0,+∞)
• B：[1,+∞)
• C：(-∞,1]
• D：(-∞,0)

答 案：C

解 析：本题主要考查的知识点为函数的值域. y=-x²+2x=1-(x-1)²≤1，故原函数的值域为(-∞,1]

4、在△ABC中,已知2B= A+C,= ac,则B-A=（）  

• A：0
• B：
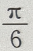
• C：
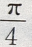
• D：

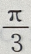
答 案：A

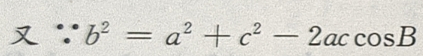
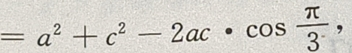
解 析：在△ABC中,A+B+C=π，A+C=π-B，① 因为2B=A+C，② 由①②得2B=π-B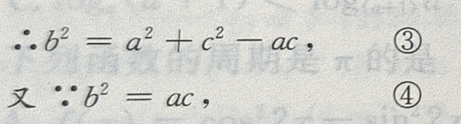， 由③④得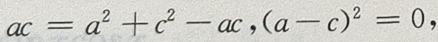a=c。所以A=C，又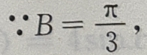所以△ABC为等边三角形，则B-A=0  

主观题

1、已知A（1，4），B（3，8），C（4，10）。求证A、B、C三点共线。  

答 案：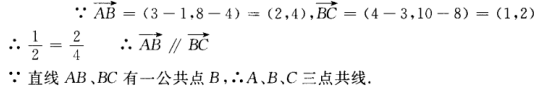

2、cos20°cos40°cos80°的值。

答 案：

3、某气象预报站天气预报的准确率为80%，计算（1）5次预报中恰有4次准确的概率； （2）5次中至少有次准确的概率.(计算结果保留两个有效数字).  

答 案：  把每次预报看做一次试验，“预报结果准确”看成事件P（A）=0.8，本题就相当于在5次独立重复试验中求A恰好发生4次（或至少4次）的概率，此题属于独立重复试验，由公式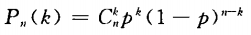来求解。 （1）n=5；p=0.8；k=4 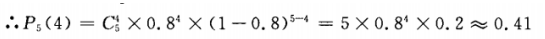即恰有4次准确的概率为0.41. (2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即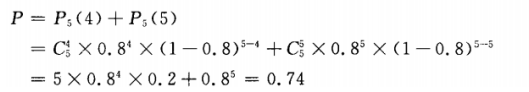 即至少有4次准确的概率为0.74。  

4、求（1+tan10°）（1+tan35°）的值。  

答 案：原式=1+tan10°+tan35°+tan10°·tan35°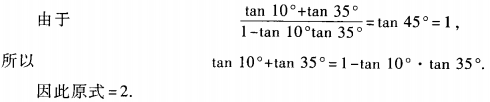

填空题

1、已知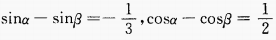，则=______。  

答 案：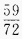

解 析：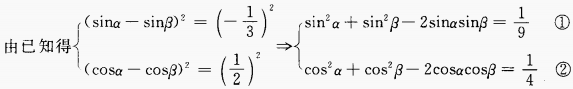

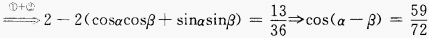
2、函数y=x⁴-2x²+5,x∈[-2,2]上的最小值______，最大值______。

答 案：4；13

解 析：y=x⁴-2x²+5,y'=4x³-4x