2025年成考高起点每日一练《数学(理)》2月13日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、函数y=sinx+cosx(x∈R)的最小正周期为()。
- A:2π
- B:π
- C:
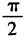
- D:
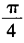
答 案:A
解 析: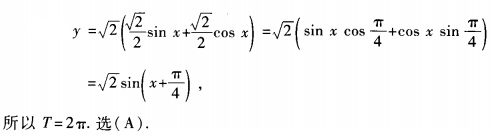
2、(a+2b)n展开式中,若第3项的二项式系数是105,则n=()。
- A:14
- B:15
- C:16
- D:17
答 案:B
解 析:展开式中,第3项的二项式系数是 即n2-n-210=0,解得n=15.n=-14(含去).(答案为B)
即n2-n-210=0,解得n=15.n=-14(含去).(答案为B)
3、要得到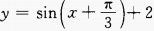 的图像,只需将y=sinx的图像().
的图像,只需将y=sinx的图像().
- A:向左平移
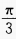 ,再向上平移2个单位
,再向上平移2个单位 - B:向左平移
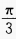 ,再向下平移2个单位
,再向下平移2个单位 - C:向右平移
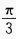 ,再向上平移2个单位
,再向上平移2个单位 - D:向右平移
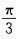 ,再向下平移2个单位
,再向下平移2个单位
答 案:A
解 析: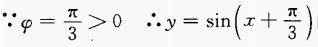 的图像是由y=sinx的图像向左平移
的图像是由y=sinx的图像向左平移 个单位,再向上平移2个单位而得到
个单位,再向上平移2个单位而得到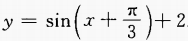
4、已知焦点在x轴上的椭圆 的焦距等于2则该椭圆上任一点P到两焦点的距里之和为()。
的焦距等于2则该椭圆上任一点P到两焦点的距里之和为()。
- A:8
- B:

- C:4
- D:

答 案:B
解 析:由题意可知a2=m,b2=4,2c=2,则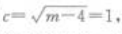 ,解得。a2=m-5,则该椭圆上任一点P到两焦点的距离之和为.
,解得。a2=m-5,则该椭圆上任一点P到两焦点的距离之和为.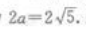 (答案为B)
(答案为B)
主观题
1、空间有四个点,如果其中任何三点不在同一直线上,可以确定几个平面?
答 案:根据公理,在所给定的四点中任取三点,可确定一个平面,由组合公式 所以共可确定四个平面。
所以共可确定四个平面。
解 析:空间有n个点,如果其中任何三点不在同一直线上,可以确定 个平面。
个平面。
2、在△ABC中,B=120°,BC=4,△ABC的面积为 ,求AC.
,求AC.
答 案:由△ABC的面积为 得
得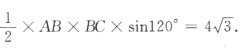 所以AB =4.因此
所以AB =4.因此 所以
所以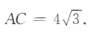
3、设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。
答 案:由已知得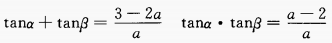

4、已知数列 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。
答 案:

填空题
1、已知关于t的二次方程t2-6tsinθ+tanθ=0(0<θ<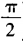 )的两根相等,则sinθ+cosθ的值等于______。
)的两根相等,则sinθ+cosθ的值等于______。
答 案: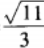
解 析: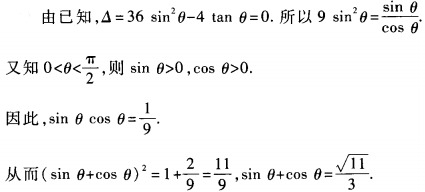
2、在△ABC中,已知a=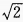 +
+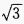 ,则bcosC+ccosB=______。
,则bcosC+ccosB=______。
答 案: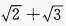
解 析:由余弦定理得,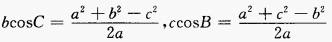
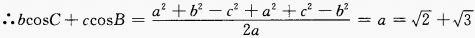
精彩评论