2025年成考高起点每日一练《数学(文史)》2月16日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、设集合M={x||x-2||<2},N={0,1,2,3,4},则M∩N=()
- A:{2}
- B:{0,1,2}
- C:{1,2,3}
- D:{0,1,2,3,4}
答 案:C
解 析:解得M={x||x-2||<2}={x|-2<x-2<2}={x|0<x<4},故M∩N={1,2,3}.
2、用列举法表示集合{(x,y)|x+2y=7且x,y为正整数},结果是()。
- A:{x=5,3,1,y=1,2,3}
- B:{(5,1),(3,2)(1,3)}
- C:{(1,5),(2,3),(3,1)}
- D:{(7,0)(5,1)(3,2)(1,3)}
答 案:B
3、在△ABC中,三边为a、b、c,∠B=60°,则 的值是()
的值是()
- A:大于零
- B:小于零
- C:等于零
- D:不能确定
答 案:C
解 析:由已知用余弦定理得: 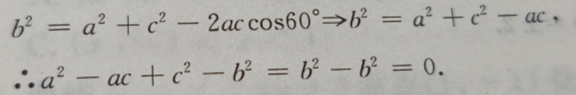
4、甲坛有8个小球,乙坛有4个小球,所有小球颜色各不相同,现从甲坛中取2个小球,乙坛中取1个小球,则取出3个球的不同取法共有()。
- A:224种
- B:112种
- C:32种
- D:1320种
答 案:B
解 析:C8(2)×C4(1)=112(种)。
主观题
1、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35° 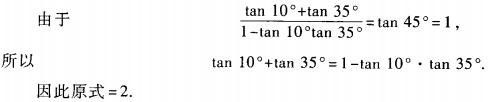
2、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
3、设函数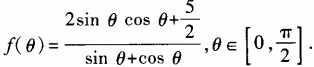 (1)求
(1)求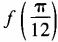 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
4、已知lg2=a,lg3=b,求lg0.15关于a,b的表达式。
答 案: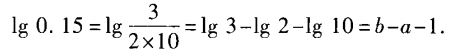
填空题
1、在△ABC中,已知AB=3,BC=5,AC=7,则cosB=______。
答 案: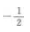
2、设 则
则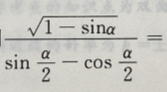
答 案:-1
解 析: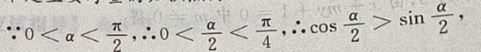
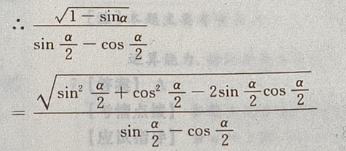
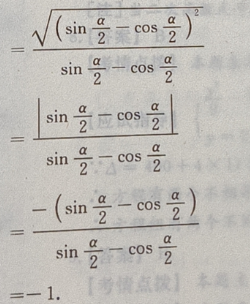
精彩评论