2025年成考高起点每日一练《数学(文史)》2月17日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知二次函数y=x2+ax+1在区间[1,+∞)上为递增函数,则实数a的取值范围是( )
- A:a≥-2
- B:a≤-2
- C:a≥-1
- D:a≤-1
答 案:A
解 析:先配方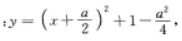 可知其图像的对称轴为
可知其图像的对称轴为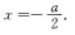 画出其图像的草图,即可得出
画出其图像的草图,即可得出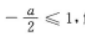 解得a≥-2
考点 本题主要考查二次函数的单调区间以及配方法和数形结合的思想在解题中的应用.
解得a≥-2
考点 本题主要考查二次函数的单调区间以及配方法和数形结合的思想在解题中的应用.
2、直线l1与直线l2:3x+2y-12=0的交点在x轴上,并且l1⊥l2,则l1在y轴上的截距是()。
- A:-4
- B:

- C:4
- D:

答 案:B
解 析:由于直线l2:3x+2y-12=0与x轴的交点为(4,0),斜率为 故直线l1的斜率为
故直线l1的斜率为 ,且经过(4,0),故l1的方程为y-0=
,且经过(4,0),故l1的方程为y-0= 令x=0求得
令x=0求得 ,即l1在y轴上的截距是
,即l1在y轴上的截距是 故选C。
用点斜式求得直线l1的方程,再根据直线在y轴上的截距的定义求得l1在y轴上的截距,本题主要考查用点斜式求直线的方程,直线在y轴上的截距的定义和求法,属于基础题
故选C。
用点斜式求得直线l1的方程,再根据直线在y轴上的截距的定义求得l1在y轴上的截距,本题主要考查用点斜式求直线的方程,直线在y轴上的截距的定义和求法,属于基础题
3、对任意两个集合A,B,下列命题中正确的是( )
- A:
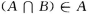
- B:
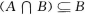
- C:
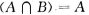
- D:
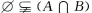
答 案:B
解 析:
4、函数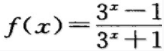 ()。
()。
- A:是偶函数
- B:是奇函数
- C:既是奇函数,又是偶函数
- D:既不是奇函数,又不是偶函数
答 案:B
主观题
1、求函数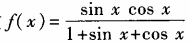 (x∈R)的最大值与最小值。
(x∈R)的最大值与最小值。
答 案:设sinx+cosx=t,则(sinx+cosx)2=t2,1+2sinxcosx=t2,sinxcosx= 于是转化为求
于是转化为求 的最值。
由所设知
的最值。
由所设知 上为增函数,故g(t)的最大值为
上为增函数,故g(t)的最大值为 最小值为
最小值为
2、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
3、设函数f(x)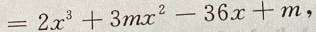 且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
答 案:(Ⅰ)由已知得f'=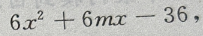 又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=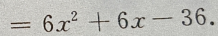 令f'(x)=0,解得
令f'(x)=0,解得 当x<-3时,f'(x)>0;
当-3
当x<-3时,f'(x)>0;
当-3
4、设椭圆的中心是坐标原点,长轴在x轴上,离心率 已知点P
已知点P 到圆上的点的最远距离是
到圆上的点的最远距离是 求椭圆的方程
求椭圆的方程
答 案:由题意,设椭圆方程为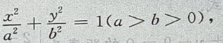 由
由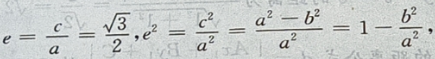
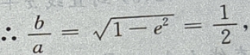 设P
设P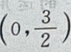 点到椭圆上任一点的距离为 d,
点到椭圆上任一点的距离为 d,
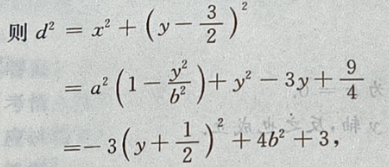
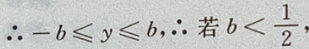 则在y=-b时,
则在y=-b时,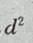 最大,即d也最大。
最大,即d也最大。
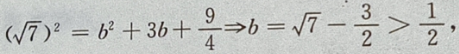

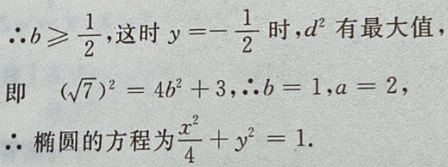
填空题
1、已知关于t的二次方程t2-6tsinθ+tanθ=0(0<θ<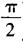 )的两根相等,则sinθ+cosθ的值等于______。
)的两根相等,则sinθ+cosθ的值等于______。
答 案:
解 析:
2、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。
答 案: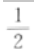
解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有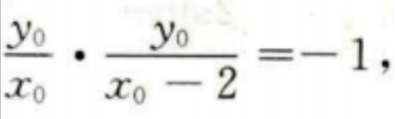 即
即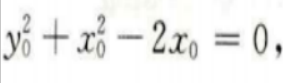
 所以
所以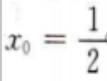 故切点横坐标为
故切点横坐标为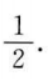
精彩评论