2025年成考高起点每日一练《数学(理)》2月18日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知sinα=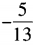，且540°＜α＜630°，则sin2α=（）。

• A：
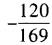
• B：
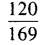
• C：
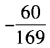
• D：

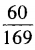
答 案：B

解 析：由已知，360°+180°＜α＜360°+270°，所以α是第三象限的角，故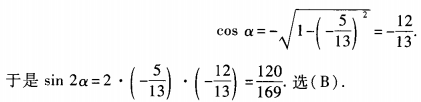

2、曲线y＝x³＋2x－1在点M（1，2）处的切线方程是（）。

• A：5x－y－3＝0
• B：x－5y－3＝0
• C：5x＋y－3＝0
• D：x＋5y－3＝0

答 案：A

解 析：由于y’=3x+2,所以曲线y=x³+2x-1在点 M(1,2)处的切线的斜率是y’|_x-1=5.所求曲线的切线方程是y-2=5(x-1),即5x-y-3=0.(答案为A)

3、（2-3i）²=（）

• A：13-6i
• B：13-12i
• C：-5-6i
• D：-5-12i

答 案：D

解 析：

4、函数y=-x²+2x的值域是（）。  

• A：[0,+∞)
• B：[1,+∞)
• C：(-∞,1]
• D：(-∞,0)

答 案：C

解 析：本题主要考查的知识点为函数的值域. y=-x²+2x=1-(x-1)²≤1，故原函数的值域为(-∞,1]

主观题

1、已知等差数列前n项和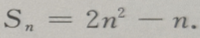 （Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和

答 案：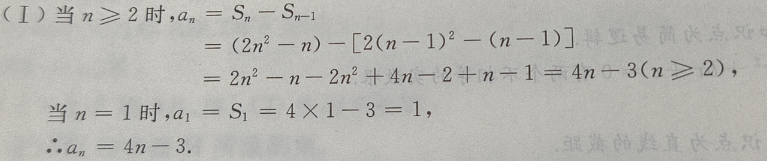  

2、当自变量为何值时，函数y=2x³-3x²-12x+21有极值，其极值为多少？  

答 案：y'=6x²-6x-12=6（x-2）（x+1） 当x<-1或x>2时，y>0，当-1 故当x=-1时有极大值，其值为f（-1）=28 当x=2时有极小值，其值为f（2）=1

3、已知数列{a_n}中，a₁=2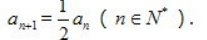， （Ⅰ）求数列{a_n}的通项公式; （Ⅱ）求数列{a_n}前5项的和 S₅

答 案：解：

4、求下列函数的最大值、最小值和最小正周期： （1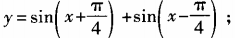）（2）y=6cosx+8sinx

答 案：  

填空题

1、在△ABC中，已知a=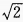+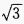，则bcosC+ccosB=______。  

答 案：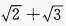

解 析：由余弦定理得，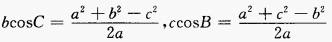  

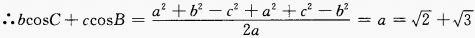
2、若tanα-cotα=1，则=______。

答 案：4

解 析：由立方差公式得,tan³α-cot³α=(tana-cotα)(tan²α+tanαcota+cot²α)(tana-cotα)[(tanα-cotα)²+3tanαcotα]=4