2025年成考高起点每日一练《数学(理)》2月19日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、以抛物线y2=8x的焦点为圆心,且与此抛物线的准线相切的圆的方程是()。
- A:(x+2)2+y2=16
- B:(x+2)2+y2=4
- C:(x-2)2+y2=16
- D:(x-2)2+y2=4
答 案:C
解 析:抛物线y2=8x的焦点,即圆心为(2,0),抛物线的准线方程是x=-2,与此抛物线的准线相切的圆的半径是r=4,与此抛物线的准线相切的圆的方程是(x-2)2+y2=16。答案为C。
2、在等比数列{an}中,a2=1,公比q=2,则a5=()。
- A:
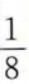
- B:
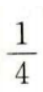
- C:4
- D:8
答 案:D
解 析:本题主要考查的知识点为等比数列。
3、设f(x)=ax+b目f(0)=-2,f(3)=4,则f(2)=()。
- A:6
- B:2
- C:1
- D:0
答 案:B
4、已知a=(-1,3),b=(-2,3),c=(0,-1),则(a·b)·c=()。
- A:(0,-11)
- B:(11,-1)
- C:10
- D:-10
答 案:A
解 析:(a·b)·c=(-1,3)·(-2.3)·(0.-1)=(2+9)·(0,-1)=11×(0,-1)=(0,-11),故应选A。 注:向量的和、差,数乘向量结果仍为向量,向量的积为数量,掌握这些结果在解选择题时可直接用排除法,会加快解题的速度以及提高解题的准确率。
主观题
1、设函数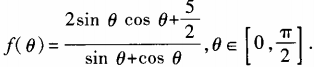 (1)求
(1)求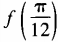 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
2、已知am=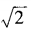 ,an=
,an=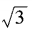 ,求a3n-4m的值。
,求a3n-4m的值。
答 案: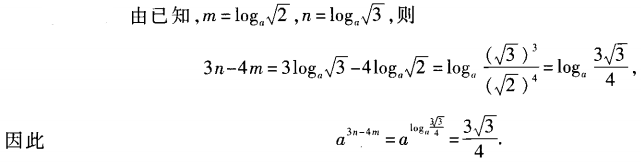
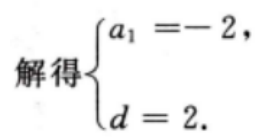
3、已知等差数列{an}中,a1+a2+a3=6,a2+a4+a5= 12求{an}的首项与公差。
答 案:因为{an}为等差数列,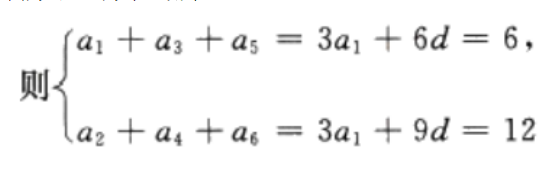
4、已知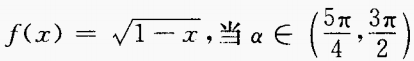 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得, 填空题 1、函数 答 案:-1 解 析: 2、在△ABC中,a=2,b= 答 案: 解 析: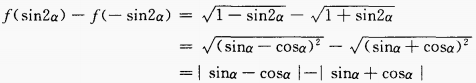
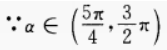 ∴sinα
∴sinα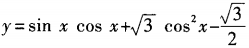 (x∈R)的最小值为______。
(x∈R)的最小值为______。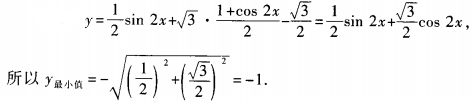
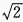 ,∠B=
,∠B=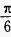 ,则∠A=______。
,则∠A=______。
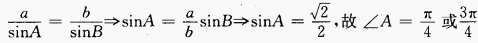
精彩评论