2025年成考高起点每日一练《数学(理)》2月20日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、一部电影在4个单位轮映,每一单位放映一场,轮映次序有()。
- A:4种
- B:16种
- C:24种
- D:256种
答 案:C
2、设log2x=a,则log2(2x2)=()。
- A:2a2+1
- B:2a2-1
- C:2a-1
- D:2a+1
答 案:D
解 析:本题主要考查的知识点为对数函数的性质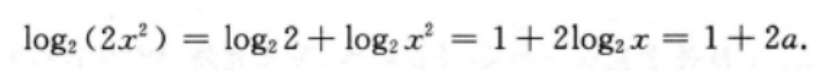
3、教室里有50人在开会,其中学生35人,家长12人,老师3人,若校长站在门外听到有人发言,那么发言人是老师或学生的概率为()。
- A:
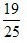
- B:
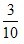
- C:
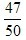
- D:
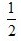
答 案:A
4、在△ABC中,c-acosB=()。
- A:bcosA
- B:acosC
- C:bcosB
- D:ccosA
答 案:A
解 析:由余弦定理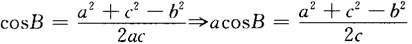
主观题
1、某工厂每月生产x台游戏机的收入为R(x)= +130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
+130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
答 案:利润 =收入-成本, L(x)=R(x)-C(x)= +130x-206-(50x+100)=
+130x-206-(50x+100)=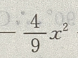 +80x-306
法一:用二次函数
+80x-306
法一:用二次函数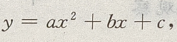 当a<0时有最大值
当a<0时有最大值
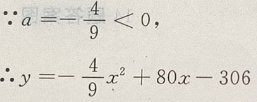 是开口向下的抛物线,有最大值
是开口向下的抛物线,有最大值
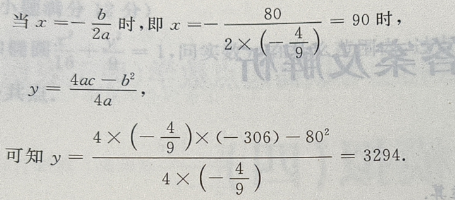 法二:用导数来求解
法二:用导数来求解
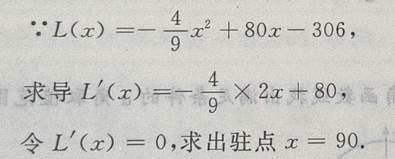 因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
2、记△ABC的内角A,B,C的对边分别为a,b,c,已知B=60°,b2=ac,求A。
答 案:由余弦定理b2=a2+c2-2accosB,可得ac=a2+c2-ac,即a2+c2-2ac=(a-c)2=0,解得a=c。 又因为B=60°,故△ABC为等边三角形,所以A=60°
3、已知a,b,c成等差数列,a,b,c+1成等比数列.若b=6,求a和c.
答 案:由已知得 解得
解得
4、已知数列 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。
答 案:

填空题
1、100件产品中有3件次品,每次抽取一件,有放回的抽取三次,恰有1件是次品的概率是______。
答 案:0.0847
解 析:由于三次抽取是独立的,每次抽取可看做是一次试验,每次试验只有两个可能结果:“正品”或“次品”,次品率为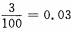 ,因此二次独立且重复试验恰有1件次品率为
,因此二次独立且重复试验恰有1件次品率为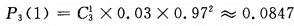
2、在△ABC中,a=2,b=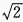 ,∠B=
,∠B=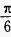 ,则∠A=______。
,则∠A=______。
答 案:
解 析: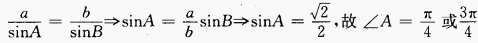
精彩评论