2025年成考高起点每日一练《数学(文史)》2月20日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设函数f（x十1)=2x+2，则f(x)=（）

• A：2x-1
• B：2x
• C：2x+1
• D：2x+2

答 案：B

解 析：f（x十1)=2x+2=2(x+1)，令t=x+1，故f(t)=2t，把t换成x，因此f(x)=2x.

2、抛物线x2=-2y+2（ ）

• A：开口向上，顶点为(0，-1)
• B：开口向上，顶点为(0，1)
• C：开口向下，顶点为(0，-1)
• D：开口向下，顶点为(0，1)

答 案：D

解 析：抛物线方程x2=-2y+2通过变化 可得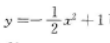 可知抛物线开口向下，顶点为（0,1） 【考点指要】本题主要考查抛物线的基本性质，是历年成人高考的常见题．

3、已知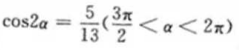,则tanα等于（）。

• A：2/3
• B：3/2
• C：-3/2
• D：-2/3

答 案：D

解 析：

4、函数y=x²+1（x＞0）的图像在（）

• A：第一象限
• B：第二象限
• C：第三象限
• D：第四象限

答 案：A

解 析：当x>0时，函数y=x²+1＞0，因此函数的图像在第一象限．

主观题

1、（1）已知tanα=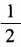 求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1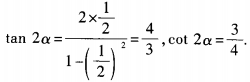） （2）由已知，得 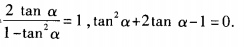解关于tanα的一元二次方程，得tanα=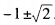

2、求证：双曲线的一个焦点到一条渐近线的距离等于虚半轴的长．  

答 案：设双曲线的方程为 则它的焦点坐标为F1(-c,0),F2(c,0),其中c²=a²+b²,渐近线方程为 令设焦点F2(c,0)到渐近线 的距离为d,则 即从双曲线的一个焦点F2(c,0)到一条渐近线的距离等于虚半 轴的长b，由上述推导过程可知，点F2到渐近线以及点F1(-c,0)到渐近线 的距离都等。 由于证明中只涉及a，b，c，而与双曲线的位置无关，所以这个结论对于任意双曲线都成立．

解 析：本题考查的是圆锥曲线与直线位置关系的推理能力，主要是用代数的方法表示几何中的问题．考生必须对曲线方程、几何性质及元素之间的关系有深刻的理解，方可解决此类综合题．这种综合性的圆锥曲线试题出现的概率比较高，要引起重视．

3、计算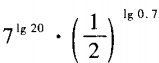  

答 案：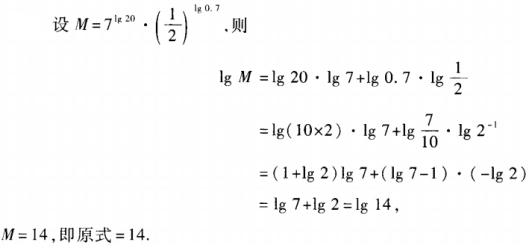

4、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

填空题

1、为了考察某种小麦的长势，从中抽取10株苗，测得苗高如下(单位：cm)：12,13，14，15，10，16，13，11，15，11． 则该品种的小麦苗高的样本方差为__________cm2．

答 案：3.6

解 析：由题中条件可得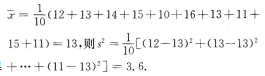 【考点指要】本题主要考查样本的平均值和方差的计算，考生只需熟记样本平均数和方差的公式即可．

2、点（4,5)关于直线y=x的对称点的坐标为（）

答 案：(5,4)

解 析：点(4,5)关于直线y=x的对称点为（5,4).