2025年成考高起点每日一练《数学(理)》2月22日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、一批产品共有5件，其中4件为正品，1件为次品，从中一次取出2件均为正品的概率为（）。  

• A：0.6
• B：0.5
• C：0.4
• D：0.3

答 案：A

解 析：本题主要考查的知识点为随机事件的概率 一次取出2件均为正品的概率为  

2、分别和两条异面直线AB、CD同时相交的两条直线AC、BD（）。

• A：相交
• B：平行
• C：是异面直线
• D：垂直

答 案：C

3、对满足a>b的任意两个非零实数，下列不等式成立的是（）  

• A：
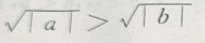
• B：
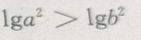
• C：
• D：

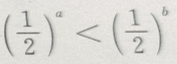
答 案：D

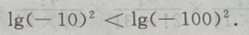解 析：A错误，例如-2>4,而 B错误，例如：-10>100,而 C错误，例如：-1>-2,而

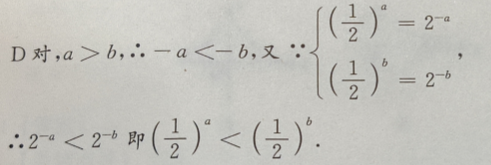
4、已知a=（-1，3），b=（-2，3），c=（0，-1），则（a·b）·c=（）。

• A：（0，-11）
• B：（11，-1）
• C：10
• D：-10

答 案：A

解 析：（a·b）·c=（-1,3）·（-2.3）·（0.-1）=（2+9）·（0，-1）=11×（0，-1）=（0，-11），故应选A。 注:向量的和、差，数乘向量结果仍为向量，向量的积为数量，掌握这些结果在解选择题时可直接用排除法，会加快解题的速度以及提高解题的准确率。

主观题

1、（1）已知tanα=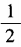，求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1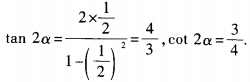）（2）由已知，得 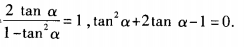解关于tanα的一元二次方程，得tanα=  

2、已知x+x^-1=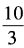，求x²+x-2的值。

答 案：由已知，得

3、已知log₅3=a，log₅4=b，求log₂₅12关于a，b的表达式。  

答 案：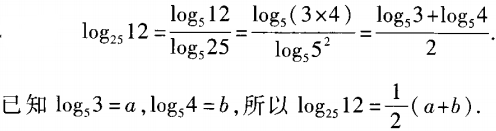

4、cos20°cos40°cos80°的值。

答 案：

填空题

1、若平面向量a=(x,1),b=(1,-2),且a//b,则x=（）  

答 案：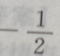

解 析：由于a//b，故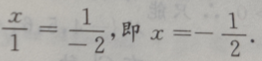

2、sin²10°+sin²20°+sin²40°+sin²50°+sin²70°+sin²80=______。

答 案：3

解 析：由互为余角的余函数值相等得 原式=(sin²10°+cos²10°)+(sin²20°+cos²20°)+(sin²40+cos²40)=1+1+1=3