2025年成考高起点每日一练《数学(文史)》2月22日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、与圆x2+y2=4关于点M(3,2)成中心对称的曲线方程是()
- A:(x-3)2+(y-2)2=0
- B:(x+3)2+(y+2)2=0
- C:(x-6)2+(y-4)2=0
- D:(x+6)2+(y+4)2=0
答 案:C
解 析:与圆关于点M成中心对称的曲线还是圆.只要求出圆心和半径,即可求出圆的方程.圆X2+y2=4的圆心(0,0)关于点M(3,2)成中心对称的点为(6,4),所以所求圆的圆心为(6,4),半径与对称圆的半径相等,所以所求圆的方程为(x-6)2+(y-4)2=4。
2、函数y=cos2x的最小正周期是()。
- A:6π
- B:4π
- C:2π
- D:π
答 案:D
3、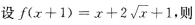 ( )
( )
- A:
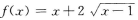
- B:

- C:
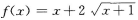
- D:
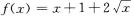
答 案:A
解 析:当已知ƒ(x+1)求ƒ(x)时,一般都用变量代换法,设x+1=t,则x=t-1,代入原式中得f(t)=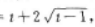 再将t换写成x即可
考点 本题主要考查函数的一般运算,如已知ƒ(x)求ƒ(x+1)或已知ƒ(x+1)求ƒ(x).
再将t换写成x即可
考点 本题主要考查函数的一般运算,如已知ƒ(x)求ƒ(x+1)或已知ƒ(x+1)求ƒ(x).
4、设甲:x>3,乙:x>5,则()。
- A:甲是乙的充分条件,但不是乙的必要条件
- B:甲是乙的必要条件,但不是乙的充分条件
- C:甲是乙的充分必要条件
- D:甲不是乙的充分条件,也不是乙的必要条件
答 案:B
主观题
1、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。(I)求C的方程;
(Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB。
答 案:(I)由题意,该抛物线的焦点到准线的距离为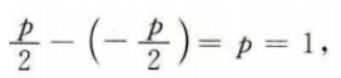 所以抛物线C的方程为y2=2x.
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得 m=
所以抛物线C的方程为y2=2x.
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得 m=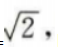 因此A点坐标为
因此A点坐标为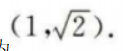 设B点坐标为
设B点坐标为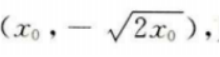
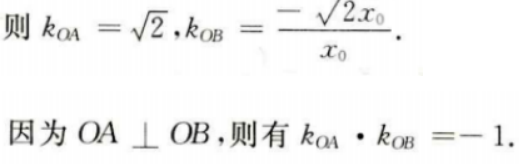

2、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数.
答 案:设每亩增种x棵,总收入味y元,则每亩种树(20+x)棵,由题意知增种x棵后每棵收入为(60-3x) 则有y=(90-3x)(20+x)
整理得y=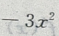 +30x+1800
配方得y=
+30x+1800
配方得y= +1875
当x=5时,y有最大值,所以每亩地最多种25棵
+1875
当x=5时,y有最大值,所以每亩地最多种25棵
3、设全集U=R,集合A={x|-5<x<5},B={x|0≤x≤7},求CUA∩B.
答 案:解:全集U=R,A={x|-5<x<5},B={X|0≤x≤7},因为CuA={x|x≤-5或x≥5},所以CuA∩B={x|x≤-5或x≥5}N{x|0≤x≤7}={x|5≤x≤7},如图1—10所示。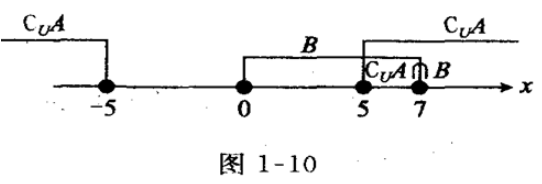
4、在△ABC中,B=120°,C=30°,BC=4,求△ABC的面积.
答 案:因为A= 180°-B-C=30°,所以AB = BC=4.因此△ABC的面积
填空题
1、任选一个不大于20的正整数,它恰好是3的整数倍的概率是()
答 案: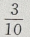
解 析:设n为不大于20的正整数的个数,则n=20,m为在这20个数中3的倍数:3,6、9、12、15、18的个数。 ∴m=6,∴所求概率=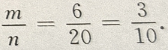
2、在△ABC中,已知AB=3,BC=5,AC=7,则cosB=______。
答 案: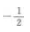
精彩评论