2025年成考专升本每日一练《高等数学二》3月23日专为备考2025年高等数学二考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、若，则。（）  

答 案：错

解 析：

单选题

1、设函数f(x)＝cos2x，则f'(x)＝（）.

• A：2sin2x
• B：－2sin2x
• C：sin2x
• D：－sin2x

答 案：B

解 析：.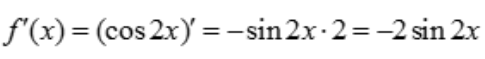

2、下列极限计算正确的是（）

• A：
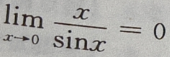
• B：
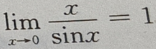
• C：
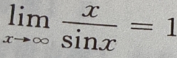
• D：

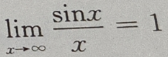
答 案：B

解 析：对于A选项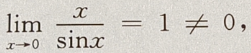：错误;对于选项B正确；对于选项C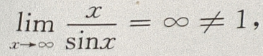错误，对于选项D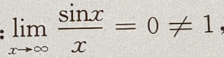错误。

主观题

1、设函数y＝f（x）是由方程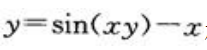确定的隐函数，求导数y′．

答 案：解：方程两边同时关于x求导得

2、设，其中f为可微函数．证明：．

答 案：证：因为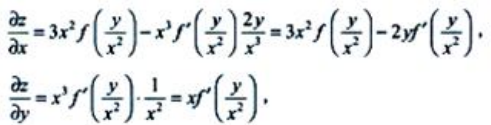所以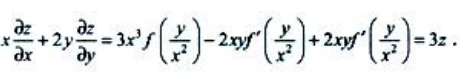

填空题

1、若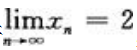，则（）．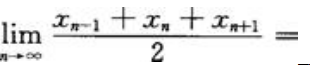

答 案：3

解 析：因为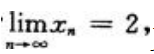又因为数列有无极限和其极限值是多少与数列中含有限项的个数无关，所以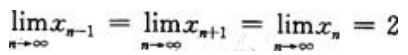，则原式＝3．

2、曲线y=lnx在点(1,0)处的切线方程为（）  

答 案：y=x-1

解 析：因为y=lnx,y'=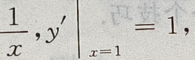所以曲线y=lnx在点(1,0)处的切线方程为y=x-1

简答题

1、证明：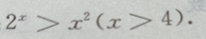

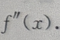答 案：令则由于此式不便判定符号，故再求出又因所以f'(x)单调增加，故f'(x)>f'(4)=-8=8(2ln2-1)=8(ln4-1)>0, 得到f(x)单调增加，故f(x)>f(4),即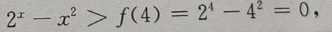因此

2、设z=x（x，y）由方程e^z-xy²+sin（y+z）=0确定，求Dz。  

答 案：本题考查的知识点是二元隐函数全微分的求法。