2025年成考专升本每日一练《高等数学二》3月25日专为备考2025年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、二元函数 的定义域为().
的定义域为().
- A:1≤x2+y2≤4
- B:1<x2+y2≤4
- C:1≤x2+y2<4
- D:1<x2+y2<4
答 案:B
解 析:对数的真数部分大于0,即x2+y2-1>0;根号内大于等于0,即4-x2-y2≥0.
2、设函数z=ln(xy),则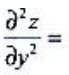 ().
().
- A:
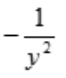
- B:
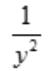
- C:

- D:
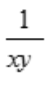
答 案:A
解 析: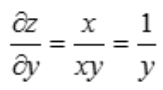 ,
,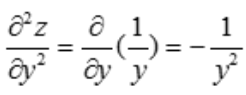 .
.
主观题
1、已知离散型随机变量X的概率分布为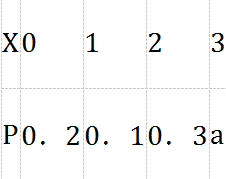 (1)求常数a;
(1)求常数a;
(2)求X的数学期望EX和方差DX.
答 案:解:(1)因为0.2+0.1+0.3+a=1,所以a=0.4;(2)EX=0×0.2+1×0.1+2×0.3+3×0.4=1.9;DX=(0-1.9)2×0.2+(1-1.9)2×0.1+(2-1.9)2×0.3+(3-1.9)2×0.4=1.29.
2、设函数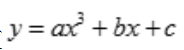 ,在点x=1处取得极小值-1,且点(0,1)是该曲线的拐点,试求常数a,b,c及该曲线的凹凸区间.
,在点x=1处取得极小值-1,且点(0,1)是该曲线的拐点,试求常数a,b,c及该曲线的凹凸区间.
答 案:解: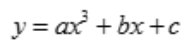 ,则
,则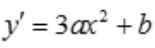 ,
,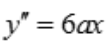 .由y(1)=-1,y(0)=1,y'(1)=0,得方程组
.由y(1)=-1,y(0)=1,y'(1)=0,得方程组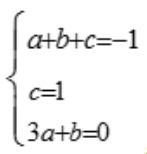 ,解得a=1,b=-3,c=1,所以
,解得a=1,b=-3,c=1,所以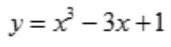 ,当x>0时,y''>0,则曲线的凹区间为(0,+∞);当x<0时,y''<0,则曲线
,当x>0时,y''>0,则曲线的凹区间为(0,+∞);当x<0时,y''<0,则曲线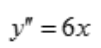 的凸区间为(-∞,0).
的凸区间为(-∞,0).
填空题
1、当x→0时,f(x)与sin2x是等价无穷小量,则 ().
().
答 案:1
解 析:根据等价无穷小定义,可知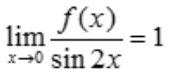 .
.
2、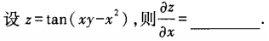
答 案: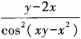
解 析:z对x求偏导时应视y为常数,并用一元函数求导公式计算,即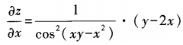 。
。
简答题
1、设函数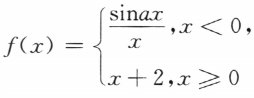 在x=0处连续,求a.
在x=0处连续,求a.
答 案:因为f(x)在x=0处连续,所以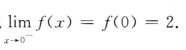 由于
由于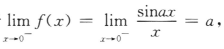 所以a=2.
所以a=2.
2、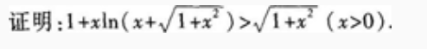
答 案: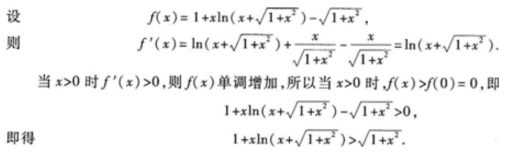
精彩评论