2025年成考高起点每日一练《数学(理)》3月29日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、若P为正方体A1C中A1B1棱上的中点,则过P、B、D三点的平面与AA1B1B面所成的二面角的余弦值为()。
- A:

- B:
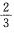
- C:
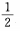
- D:
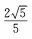
答 案:B
解 析:
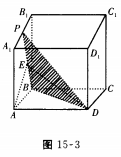
2、设F1和F2为双曲线的两焦点,点P在双曲线上,则||PF2|-|PF2||=()。
- A:4
- B:2
- C:1
- D:
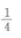
答 案:A
解 析:由题意有a2=4.a=2,由双曲线的定义,可知||PF2|-|PF2||=2a=4.(答案为A)
3、已知α∩β=a,b⊥β,b在α内的射影是b’,那么b'和α的关系是()
- A:b'//α
- B:b'⊥α
- C:b'与α是异面直线
- D:b'与α相交成锐角
答 案:B
解 析: ∴由三垂线定理的逆定理知,b在α内的射影b'⊥α,故选B
∴由三垂线定理的逆定理知,b在α内的射影b'⊥α,故选B
4、从点M(x,3)向圆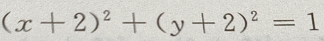 作切线,切线的最小值等于()
作切线,切线的最小值等于()
- A:4
- B:
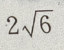
- C:5
- D:
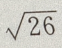
答 案:B
解 析:如图,相切是直线与圆的位置关系中的一种,此题利用圆心坐标、半径,求出切线长. 由圆的方程知,圆心为B(-2,-2),半径为1,设切点为A,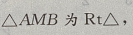 由勾股定理得,
由勾股定理得,
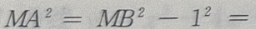

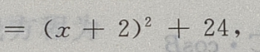
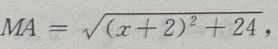 当x+2=0时,MA取最小值,最小值为
当x+2=0时,MA取最小值,最小值为

主观题
1、已知关于x的二次方程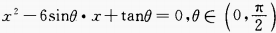 的两根相等,求sinθ+cosθ的值。
的两根相等,求sinθ+cosθ的值。
答 案:

2、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
答 案:由已知,得 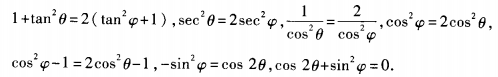
3、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35°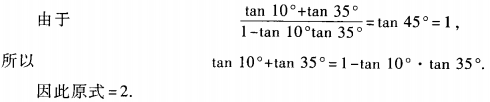
4、已知等差数列前n项和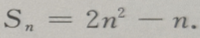 (Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
(Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
答 案: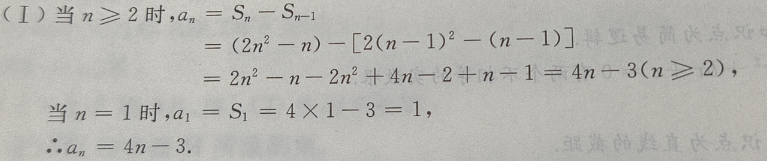

填空题
1、长方体的长、宽、高分别为2,3,6,则该长方体的对角线长为()
答 案:7
解 析:由题可知长方体的底面的对角线长为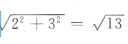 ,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为
,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为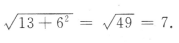
2、不等式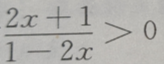 的解集为()
的解集为()
答 案: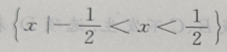
解 析:

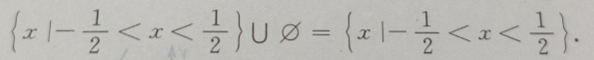
精彩评论