2025年成考高起点每日一练《数学(理)》4月4日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、下列函数中,为偶函数的是()。
- A:
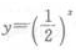
- B:
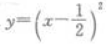
- C:
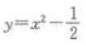
- D:
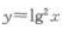
答 案:C
解 析:根据函数的奇偶性的定义可知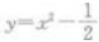 为偶函数
为偶函数
2、抛物线y2=4x上一点P到焦点F的距离是10,则点P坐标是()。
- A:(9,6)
- B:(9,±6)
- C:(6,9)
- D:(±6,9)
答 案:B
解 析:抛物线y2=4x的焦点为F(1,0),设点P坐标是(z,y),则有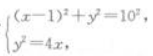 解方程组,得x=9,y=±6,即点P坐标是(9,±6).(答案为B)
解方程组,得x=9,y=±6,即点P坐标是(9,±6).(答案为B)
3、设函数f(x)=ex,则f(x-a)·f(x+a)=()。
- A:f(x2-a2)
- B:2f(x)
- C:f(x2)
- D:f2(x)
答 案:D
4、函数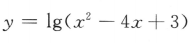 的定义域是()
的定义域是()
- A:{x|-3<x<-1}
- B:{x|x<-3或x>-1}
- C:{x|1<x<3}
- D:{x|x<1或x>3}
答 案:D
解 析:由对数函数的性质可知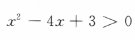 ,解得x>3或x<1,因此函数的定义域为{x|x<1或x>3}
,解得x>3或x<1,因此函数的定义域为{x|x<1或x>3}
主观题
1、求将抛物线y=x2-2x-3平移到顶点与坐标原点重合时的函数解析式。
答 案:
2、建筑一个容积为8000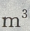 ,深为6m的长方体蓄水池,池壁每
,深为6m的长方体蓄水池,池壁每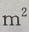 的造价为15元,池底每
的造价为15元,池底每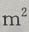 的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
答 案: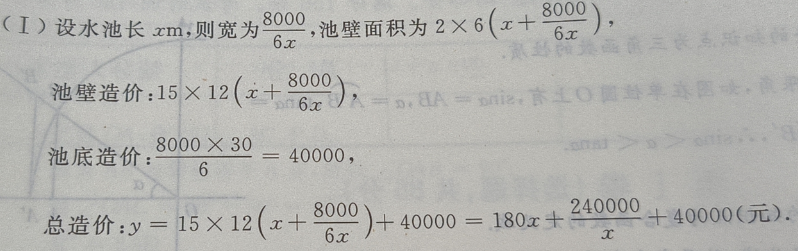

3、cos20°cos40°cos80°的值。
答 案:
4、空间有四个点,如果其中任何三点不在同一直线上,可以确定几个平面?
答 案:根据公理,在所给定的四点中任取三点,可确定一个平面,由组合公式 所以共可确定四个平面。
所以共可确定四个平面。
解 析:空间有n个点,如果其中任何三点不在同一直线上,可以确定 个平面。
个平面。
填空题
1、点B(4,-5)按向量a平移后的对应点B0(-4,7),则a的坐标是______。
答 案:(-8,12)
解 析:由平移公式得-4=4+a1,7=-5+a2→a1=-8,a2=12 ∴a的坐标是(-8,12)。
2、 的展开式是()
的展开式是()
答 案: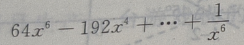
解 析: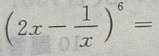
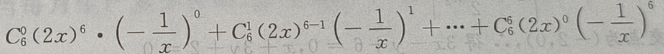

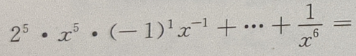
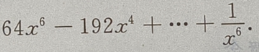
精彩评论