2025年成考高起点每日一练《数学(理)》4月6日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、如果不共线的向量a和b有相等的长度,则(a+b)(a-b)=()
- A:0
- B:1
- C:-1
- D:2
答 案:A
解 析:(a+b)(a-b)=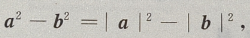
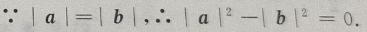
2、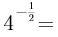 ( )
( )
- A:-2
- B:
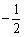
- C:
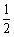
- D:2
答 案:C
3、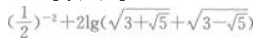 ()。
()。
- A:3
- B:4
- C:5
- D:6
答 案:C
解 析: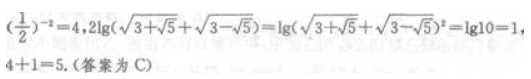
4、以椭圆 上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于()。
上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于()。
- A:

- B:

- C:

- D:

答 案:A
解 析:由椭圆方程 可知,a2=9,b2=4
可知,a2=9,b2=4 ,则椭圆上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于
,则椭圆上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于
主观题
1、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。 (I)求C的方程; (Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
答 案:(I)由题意,该抛物线的焦点到准线的距离为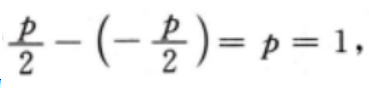 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得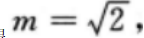 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为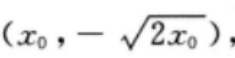 则
则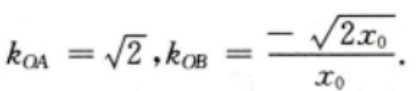 因为
因为 则有
则有 即
即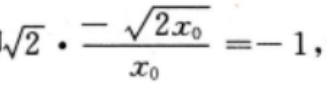 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
2、已知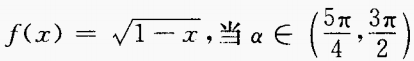 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得, 3、已知A(1,4),B(3,8),C(4,10)。求证A、B、C三点共线。
答 案: 4、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得 答 案:如图, 填空题 1、已知A(0,1),B(1,2),存在一点P是 答 案: 解 析: 2、y=cos22x的最大值是______,最小值______,周期T=______。
答 案:1;0; 解 析: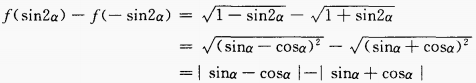
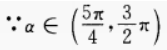 ∴sinα
∴sinα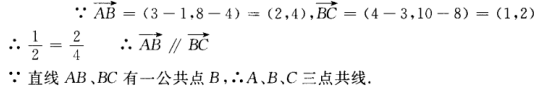
 AB=120m,求河的宽
AB=120m,求河的宽

 ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
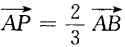 ,则点P的坐标是______。
,则点P的坐标是______。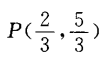
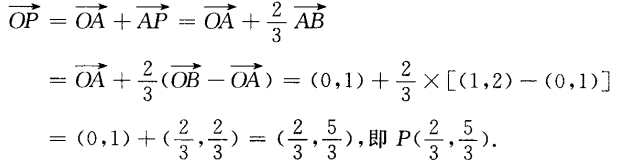
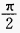
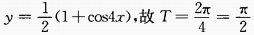 ,最大值为
,最大值为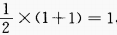 ,最小值为
,最小值为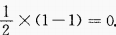
精彩评论