2025年成考高起点每日一练《数学(文史)》4月7日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、 则()。
则()。
- A:

- B:b∉M
- C:

- D:{b}∈M
答 案:C
2、下列各式的值为零的是()。
- A:00
- B:log11
- C:
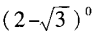
- D:log2|-1|
答 案:D
解 析:00和log11均没有意义,可排除(A)、(B),而(2-)0=1。故选D。
3、设M=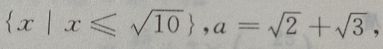 那么()
那么()
- A:
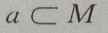
- B:
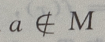
- C:
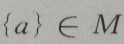
- D:
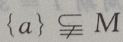
答 案:D
解 析: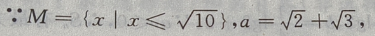 M是集合,a为元素,{a}为集合,元素与集合的关系是
M是集合,a为元素,{a}为集合,元素与集合的关系是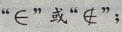 集合与集合的关系是
集合与集合的关系是

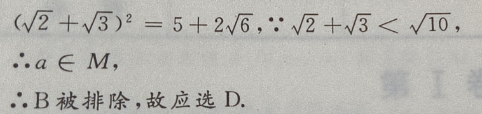
4、若向量a=(x,-2),b=(-2,1),且a//b,则x=()。
- A:-4
- B:-1
- C:1
- D:4
答 案:D
主观题
1、已知F是椭圆 的右焦点,点M在抛物线y2=2px(p>0)上O为坐标原点,且△MOF为正三角形.
(Ⅰ)求P的值; (Ⅱ)求抛物线的焦点坐标和准线方程.
的右焦点,点M在抛物线y2=2px(p>0)上O为坐标原点,且△MOF为正三角形.
(Ⅰ)求P的值; (Ⅱ)求抛物线的焦点坐标和准线方程.
答 案:(Ⅰ)由椭圆方程可知,椭圆的长半轴a=5,短半轴,则椭圆的半焦距 即椭圆的右焦点F的坐标为
(4.0).
即椭圆的右焦点F的坐标为
(4.0). 如图,因为△MOF为正三角形,OF=4,过M作MN⊥OF于N点,
如图,因为△MOF为正三角形,OF=4,过M作MN⊥OF于N点, 【考点指要】本题主要考查椭圆、抛物线的概念,要求考生掌握它们的标准方程和性质,会用它们解决有关的问题.
【考点指要】本题主要考查椭圆、抛物线的概念,要求考生掌握它们的标准方程和性质,会用它们解决有关的问题.
2、设函数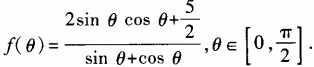 (1)求
(1)求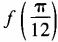 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
3、cos20°cos40°cos80°的值。
答 案:
4、一艘渔船在航行中遇险,发出警报,在遇险地点西南10海里处有一艘货轮,接收到报时,发现遇险渔船正以9海里/小时的速度与沿南偏东75°方向向某小岛靠近,如果要在40分内将这艘渔船救出,求货轮航行的方向和速度。
答 案:货轮沿东偏北21.8°的方向,以21海里/小时的船速航行。
填空题
1、直线 的倾斜角的度数为()
的倾斜角的度数为()
答 案:60°
解 析:由题意知直线的斜率为 设直线的倾斜角为α,则tanα=
设直线的倾斜角为α,则tanα= 由0°≤α≤180°,故α=60°
由0°≤α≤180°,故α=60°
2、已知点P(-3,1)为角α终边上一点,则cos(2α-π)的值等于______。
答 案: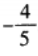
解 析:因为cos(2α-π)=cos(π-2α)=-cos2α。由已知,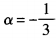 所以
所以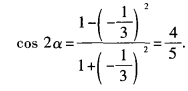
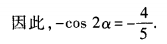
精彩评论