2025年成考专升本每日一练《高等数学一》4月8日专为备考2025年高等数学一考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

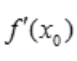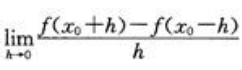1、设函数f(x)在x＝x₀处可导，且＝2，则等于（）。

• A：
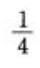
• B：2
• C：0
• D：4

答 案：D

解 析：依题意得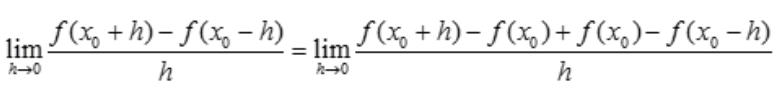

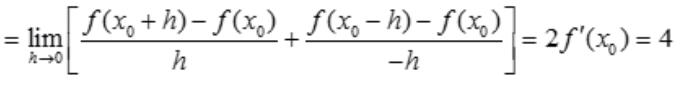
2、微分方程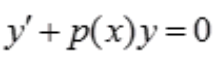的通解为（）。

• A：
• B：y＝
• C：y＝
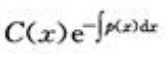
• D：y＝

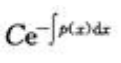
答 案：D

解 析：由一阶线性微分方程的通解公式可知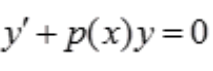的通解为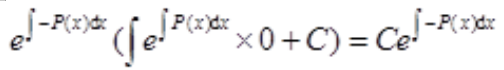

3、设有直线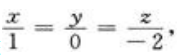则该直线（）。

• A：过原点且垂直于x轴
• B：过原点且垂直于y轴
• C：过原点且垂直于z轴
• D：不过原点也不垂直于坐标轴

答 案：B

解 析：将原点坐标（0，0，0）代入方程，等式成立，则直线过原点；由于所给直线的方向向量s＝（1，0，－2），而y轴正方向上的单位向量i＝（0，1，0），s·i＝1×0＋0×1＋（－2）×0＝0，因此s⊥i，即所给直线与y轴垂直。

主观题

1、求

答 案：解：。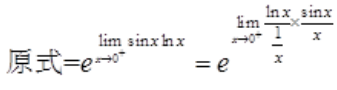

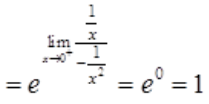2、求函数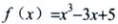的极大值与极小值。

答 案：解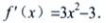：令f′(x)＝0，解得x₁＝－1；x₂＝1又f″(x)＝6x,可知f″(-1)＝－６＜0，f″(1)＝6＞0
故x＝－1为f（x）的极大值点，极大值为7
x＝1为f（x）的极小值点，极小值为3。

3、计算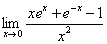

答 案：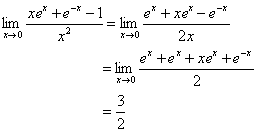

填空题

1、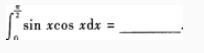  

答 案：

解 析：

2、设y＝x³＋2，则y''=（）。

答 案：6x

解 析：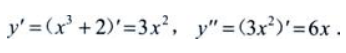

3、设函数f(x)满足f’(1)=5，则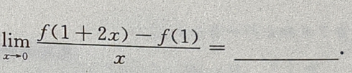

答 案：10

解 析：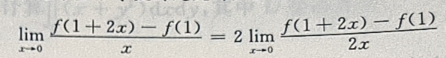

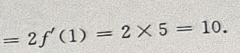
简答题

1、讨论级数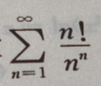敛散性。

答 案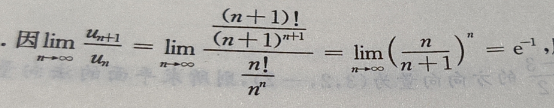：所以级数收敛。