2025年成考高起点每日一练《数学(理)》4月9日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设甲：二次不等式x²+px+q＞0的解集为空集合；乙：△=p²-4q＜0则（）。

• A：甲是乙的必要条件，但不是乙的充分条件
• B：甲是乙的充分条件，但不是乙的必要条件
• C：甲不是乙的充分条件，也不是乙的必要条件
• D：甲是乙的充分必要条件

答 案：D

解 析：由于二次不等式x²+px+q＞0的解集为空集合△=p2-4q＜0,则甲是乙的充分必要条件(答案为 D)

2、下列四个命题中正确的是（）。 ①已知a，b，c三条直线，其中a，b异面，a//c，则b，c异面。
②若a与b异面，b与c异面，则a与c异面。
③过平面外一点与平面内一点的直线，和平面内不经过该点的直线是异面直线。
④不同在任何一个平面内的两条直线叫异面直线。

• A：③④
• B：②③④
• C：①②③④
• D：①②

答 案：A

解 析：①b与c可相交，②a与c可以有平行、相交、异面三种位置关系。答案为A。  

3、如果球的大圆面积增为原来的4倍，则该球的体积就增为原来的（）。

• A：4倍
• B：8倍
• C：12倍
• D：16倍

答 案：B

解 析：

4、一个袋子中装有标号分别为1，2，3，4的四个球，采用有放回的方式从袋中摸球两次，每次摸出一个球，则恰有一次摸出2号球的概率为（）。

• A：
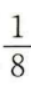
• B：
• C：
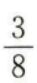
• D：

答 案：C

解 析：本题主要考查的知识点为独立重复试验的概率。 所求概率为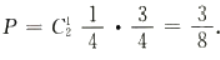

主观题

1、在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量和关于基底{a,b,c}的分解式; （Ⅱ）求证： （Ⅲ）求证：  

答 案：（Ⅰ）由题意知(如图所示)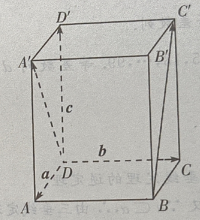  

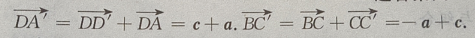
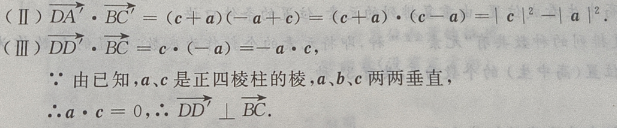
2、设a为实数，且tanα和tanβ是方程ax²+（2a-3）x+（a-2）=0的两个实根，求tan（α+β）的最小值。

答 案：由已知得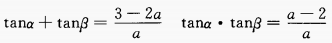

3、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。

答 案：由已知，得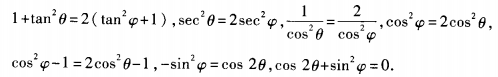

4、设（0＜α＜π），求tanα的值。

答 案：

填空题

1、长方体的长、宽、高分别为2,3,6，则该长方体的对角线长为（）

答 案：7

解 析：由题可知长方体的底面的对角线长为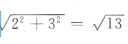，则在由高、底面对角线、长方体的对角线组成的三角形中，长方体的对角线长为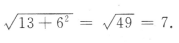

2、化简sin（x+y）-2cosxsiny=______.  

答 案：sin（x-y）

解 析：原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin（x-y）