2025年成考高起点每日一练《数学(文史)》4月9日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、函数y=cos⁴x-sin⁴x（x∈R）的最小正周期为（）。

• A：
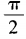
• B：π
• C：2π
• D：4π

答 案：B

解 析：y=（cos²x+sin²x）（cos²x-sin²x）=cos2x， 所以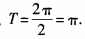

2、若|a|=4，|b|=，且a•b=则=（）。

• A：120°
• B：150°
• C：60°
• D：30°

答 案：B

3、已知二次函数y=x²+ax+1在区间[1，+∞)上为递增函数，则实数a的取值范围是（　）

• A：a≥-2
• B：a≤-2
• C：a≥-1
• D：a≤-1

答 案：A

解 析：先配方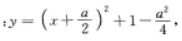可知其图像的对称轴为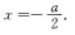画出其图像的草图，即可得出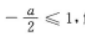解得a≥-2 考点 本题主要考查二次函数的单调区间以及配方法和数形结合的思想在解题中的应用．

4、函数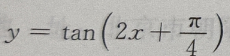的最小正周期为

• A：
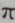
• B：
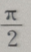
• C：
• D：

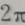
答 案：B

解 析：由正切函数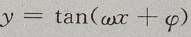的最小正周期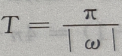得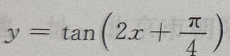的最小正周期为

主观题

1、已知a^m=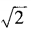，aⁿ=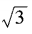，求a^3n-4m的值。  

答 案：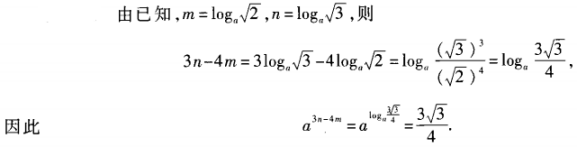

2、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。

答 案：(I)由题意,该抛物线的焦点到准线的距离为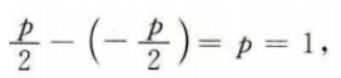 所以抛物线C的方程为y²=2x. (Ⅱ)因A(l,m)(m>0)为C上一点,故有m²=2, 可得 m=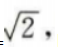因此A点坐标为 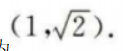设B点坐标为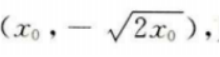

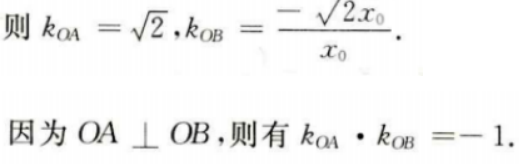
3、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

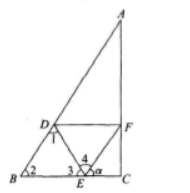
4、在△ABC中，已知AB=2,BC=1,CA=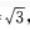 点D,E,F分别在AB,BC,CA边上，△DEF为正三角形，记∠FEC为α，如果sinα= 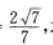求△DEF的边长。

答 案：解析:由AB=2，BC=1,CA=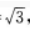 得BC²=CA²=AB²,因此∠C=90°，如图所示。 因为sinA= 所以∠A=30°，于是∠b=60°。 设正△DEF边长为l，已知AB=2,sinα=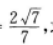 由此EC=lcosα 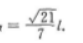有图知，∠1+∠2+∠3=180°（三角形内角和）； ∠3+∠4+α=180°，因为∠2-∠4=60°，所以∠1=α。 【考点指要】本题主要考查三角函数的概念、同角三角函数的关系及正弦定理，这些均是考试大纲要求掌握的重要概念，并要求能达到灵活应用的程度，此类题是在成人高考中出现频率较高的题型，

填空题

1、甲、乙、丙三位教师担任6个班的课，如果每人任选两个班上课有______种不同的任课方法。  

答 案：90

2、某人投篮每次命中率为0.8，现独立投篮4次，恰好命中3次的概率是______。  

答 案：0.4096

解 析：本题试验属于独立重复试验，其概率为