2025年成考高起点每日一练《数学(理)》4月10日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、若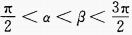，则必有（）。

• A：sinα＞sinβ
• B：cosα＞cosβ
• C：tanα＞tanβ
• D：cotα＞cotβ

答 案：A

解 析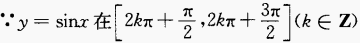： 是函数，故当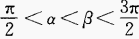时，  

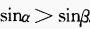
2、函数F(x)＝f(x)·sinx是奇函数，则f(x)（）。

• A：是偶函数
• B：是奇函数
• C：既是偶函数又是奇函数
• D：既不是偶函数又不是奇函数

答 案：A

解 析：因为函数F(x)=f(x)·sinx是奇函数,sinx是奇函数, 故 F(-x)=-F(x),sin(-xx)=-sinx. 即f(x)sin(-x)=-f(x)sinx,得f(x)=f(-x),则f(x)是偶函数(答案为 A)

3、过点（-2，2）与直线x+3y-5=0平行的直线是（）

• A：x+3y-4=0
• B：3x+y+4=0
• C：x+3y+8=0
• D：3x-y+8=0

答 案：A

解 析：所求直线与x+3y-5=0平行，可设所求直线为x+3y+c=0，将点（一2,2)带入直线方程，故-2+3×2+c=0，解得c=-4，因此所求直线为线为x+3y-4=0.

4、（）。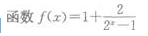

• A：是奇函数
• B：是偶函数
• C：既是奇函数，又是偶函数
• D：既不是奇函数，又不是偶函数

答 案：A

解 析：

主观题

1、试证明下列各题
（1）
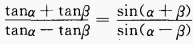
（2）

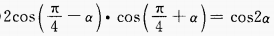
答 案：（1）化正切为正、余弦，通分即可得证。 （2）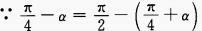

2、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。

答 案：由已知，得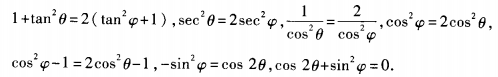

3、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

4、函数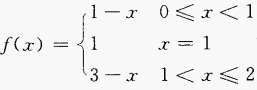在其定义域上是否连续？作出f（x）的图形。

答 案：f（x）的定义域为[0，2] 当0≤x<1时f（x）=1-x是连续的 当1 f(x)除了在x=1处不连续,在其定义域内处处连续,如图7-7.

填空题

1、若P（3，2）是连接P1（2，y）和P2（x，6）线段的中点，则x=______，y=______。  

答 案：x=4，y=-2  

解 析：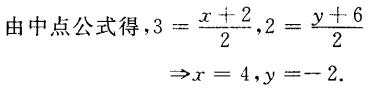

2、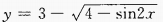的值域是______。  

答 案：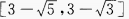

解 析：当sin2x=-1时，y最小值当 sin2x=1时,