2025年成考高起点每日一练《数学(理)》4月11日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、一部电影在4个单位轮映,每一单位放映一场,轮映次序有()。
- A:4种
- B:16种
- C:24种
- D:256种
答 案:C
2、从1、2、3、4、5、6、7、8、9这九个数字中,随机取出一个数字,这个数字是奇数的概率是()。
- A:
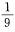
- B:
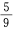
- C:
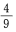
- D:
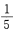
答 案:B
解 析:本题的试验是从1~9这九个数字中任取一个数字,显然选中其中任一个数字的可能 性都是相同的,属于等可能事件的概率,∵n=9,其中奇数个数m=5,∴其概率是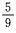 ,故选B。
,故选B。
3、函数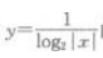 定义域为()。
定义域为()。
- A:{z|x≠0,x∈R}
- B:{x|x≠±1,x∈R}
- C:{x|x≠0,x≠±1,x∈R}
- D:{x|x∈R}
答 案:C
解 析:|x|>0,且|x|=1,得x≠0,且x≠±1。答案为C。
4、若f(x+1)=x2-2x+3,则f(x)=()。
- A:x2+2x+6
- B:x2+4x+6
- C:x2-2x+6
- D:x2-4x+6
答 案:D
解 析:f(x+1)=x2-2x+3=(x+1)2-4(x+1)+6,∴f(x)=x2-4x+6。(答案为D)
主观题
1、已知空间四边形OABC,OB=OC且∠AOB=∠AOC=θ(如图)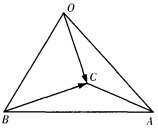 。求证:OA⊥BC。
。求证:OA⊥BC。
答 案:
2、已知等差数列{an}中,a1+a2+a3=6,a2+a4+a5= 12求{an}的首项与公差。
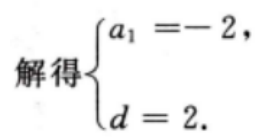
答 案:因为{an}为等差数列,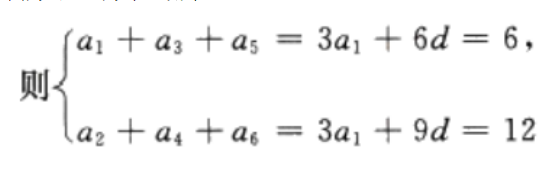
3、设A1A2A3A4A5A6为正六边形,如图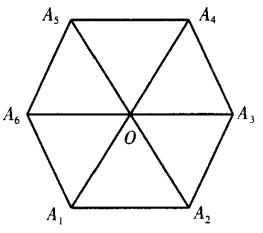 ,O为它的中心。 (1)求证:
,O为它的中心。 (1)求证: 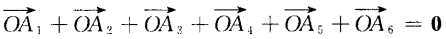 (2)
(2)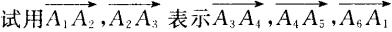
答 案:已知A1A2A3A4A5A6 为正六边形,即|A1A2|=|A3A4|=......|A6A1|.要证6个向量的和为0.只需证其中3个向量与另3个向量的长度相等、方向相反即可.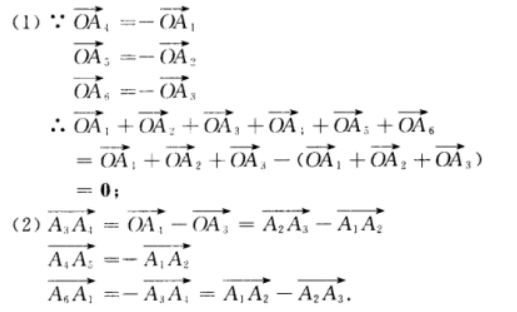
4、已知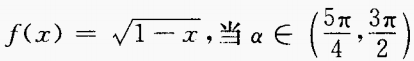 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得, 填空题 1、点B(4,-5)按向量a平移后的对应点B0(-4,7),则a的坐标是______。
答 案:(-8,12) 解 析:由平移公式得-4=4+a1,7=-5+a2→a1=-8,a2=12 ∴a的坐标是(-8,12)。
2、 答 案: 解 析:当sin2x=-1时,y最小值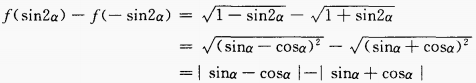
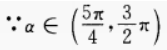 ∴sinα
∴sinα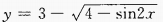 的值域是______。
的值域是______。
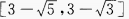
 当 sin2x=1时,
当 sin2x=1时,
精彩评论