2025年成考高起点每日一练《数学(理)》4月12日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、顶点在坐标原点，准线方程为y=4的抛物线方程式（）。

• A：
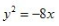
• B：
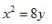
• C：
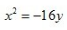
• D：

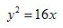
答 案：C

2、如果不共线的向量a和b有相等的长度,则(a+b)(a-b)=（）  

• A：0
• B：1
• C：-1
• D：2

答 案：A

解 析：(a+b)(a-b)=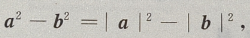

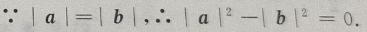
3、函数y=x²—2x+6在区间（-∞，1）、（1，+∞）分别（）。

• A：单调增加、单调减少
• B：单调减少、单调增加
• C：单调增加、单调增加
• D：单调减少、单调减少

答 案：B

解 析：方法一：用配方法把y=x²-2x+6配成完全平方式。 y=x²-2x+6=（x-1）2+5，开口向上的抛物线顶点坐标为（1，5），可得出单调区间。 方法二：用导数判定。y’=2x-2=2（x-1）
当x<1时，y’<0，单调减少；当x>1时，y>0，单调增加。

4、下列各式中，不成立的是（）。

• A：
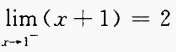
• B：
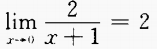
• C：
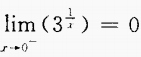
• D：

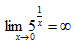
答 案：D

解 析：可用排除法，A、B、C均成立。

主观题

1、（1）已知tanα=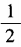，求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1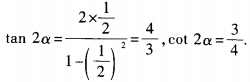）（2）由已知，得 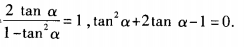解关于tanα的一元二次方程，得tanα=  

2、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．

答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得当时，f'(x)时，f'(x)＞O.故f(x）在区间单调递减，在区间单调递增．因此f(x）在时取得极小值

3、求（1+tan10°）（1+tan35°）的值。  

答 案：原式=1+tan10°+tan35°+tan10°·tan35°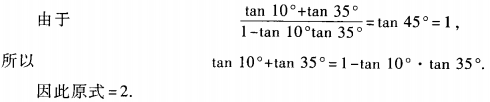

4、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由，得设A（x1,y1），B（x2,y2），则因此

填空题

1、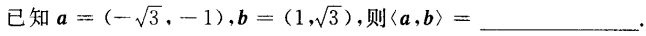  

答 案：；150°

解 析：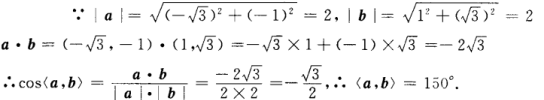

2、若tanα-cotα=1，则=______。

答 案：4

解 析：由立方差公式得,tan³α-cot³α=(tana-cotα)(tan²α+tanαcota+cot²α)(tana-cotα)[(tanα-cotα)²+3tanαcotα]=4