2025年成考高起点每日一练《数学(文史)》4月12日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、若函数y=f(z)在[a,b]上单调,则使得y=f(x+3)必为单调函数的区间是()。
- A:[a,b+3]
- B:[a+3,b+3]
- C:[a-3,b-3]
- D:[a+3,b]
答 案:C
2、某学校为新生开设了4门选修课程,规定每位新生至少要选其中3门,则一位新生不同的选课方案共有 ( )
- A:7种
- B:4种
- C:5种
- D:6种
答 案:C
3、直线l1与直线l2:3x+2y-12=0的交点在x轴上,并且l1⊥l2,则l1在y轴上的截距是()。
- A:-4
- B:

- C:4
- D:

答 案:B
解 析:由于直线l2:3x+2y-12=0与x轴的交点为(4,0),斜率为 故直线l1的斜率为
故直线l1的斜率为 ,且经过(4,0),故l1的方程为y-0=
,且经过(4,0),故l1的方程为y-0= 令x=0求得
令x=0求得 ,即l1在y轴上的截距是
,即l1在y轴上的截距是 故选C。
用点斜式求得直线l1的方程,再根据直线在y轴上的截距的定义求得l1在y轴上的截距,本题主要考查用点斜式求直线的方程,直线在y轴上的截距的定义和求法,属于基础题
故选C。
用点斜式求得直线l1的方程,再根据直线在y轴上的截距的定义求得l1在y轴上的截距,本题主要考查用点斜式求直线的方程,直线在y轴上的截距的定义和求法,属于基础题
4、设甲:四边形ABCD是平行四边形,乙:四边形ABCD是正方形,则()。
- A:甲是乙的充分条件,但不是乙的必要条件
- B:甲是乙的必要条件,但不是乙的充分条件
- C:甲是乙的充分必要条件
- D:甲不是乙的充分条件,也不是乙的必要条件
答 案:B
主观题
1、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
答 案:由已知,得 
2、已知a-a-1=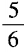 ,求a3-a-3的值。
,求a3-a-3的值。
答 案:
3、已知函数f(x)=2x3-3x2,求
(1)函数的单调区间;
(2)函数f(x)在区间[-3,2]的最大值与最小值。
答 案:
4、如图:已知在△ADC中,∠C=90°,∠D=30°,∠ABC=45°,BD=20,求AC(用小数表示,保留一位小数)

答 案:如图 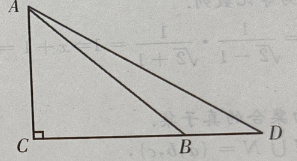
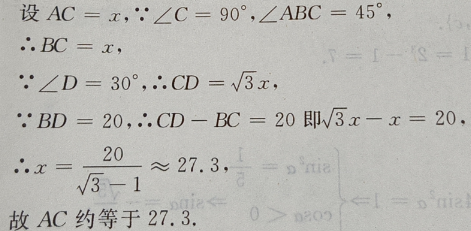
填空题
1、化简sin(x+y)-2cosxsiny=______。
答 案:sin(x-y)
解 析:原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin(x-y)
2、任选一个不大于20的正整数,它恰好是3的整数倍的概率是()
答 案: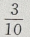
解 析:设n为不大于20的正整数的个数,则n=20,m为在这20个数中3的倍数:3,6、9、12、15、18的个数。 ∴m=6,∴所求概率=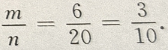
精彩评论