2025年成考高起点每日一练《数学(理)》4月14日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、设F1,F2分别是椭圆的焦点,并且B1是该椭圆短轴的一个端点,则△F1F2B1,的面积等于()。
- A:
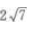
- B:
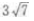
- C:
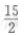
- D:2
答 案:B
解 析:
2、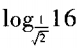 =()。
=()。
- A:8
- B:-8
- C:2
- D:-2
答 案:B
解 析:由于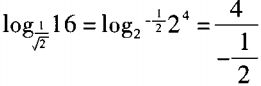 。log22=-8。故选B。
。log22=-8。故选B。
3、等差数列{an}前n项和为Sn且S10=100 ,S30=900 ,那么S50的值等于()。
- A:2400
- B:2500
- C:2700
- D:2800
答 案:B
4、直线3x-4y-9=0与圆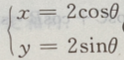 (θ为参数)的位置关系是
(θ为参数)的位置关系是
- A:相交但直线不过圆心
- B:相交但直线通过圆心
- C:相切
- D:相离
答 案:A
解 析:方法一: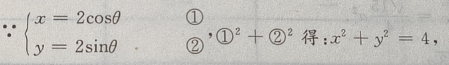 圆心O(0,0),r=2,则圆心O到直线的距离为
圆心O(0,0),r=2,则圆心O到直线的距离为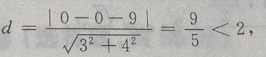 0
0
主观题
1、求下列函数的定义域: (1)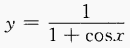
(2)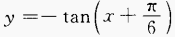
(3)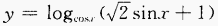
答 案:(1) 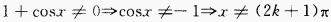 ∴函数的定义域为
∴函数的定义域为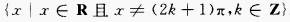 (2)
(2) 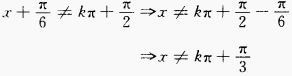 ∴函数的定义域为
∴函数的定义域为 (3)
(3)
由对数函数的性质知,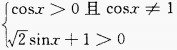
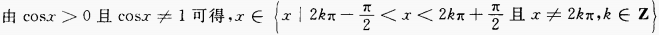
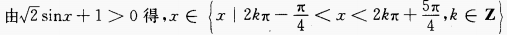 故函数的定义域为
故函数的定义域为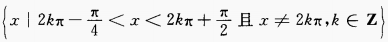
2、已知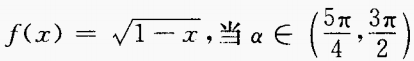 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得, 3、已知log53=a,log54=b,求log2512关于a,b的表达式。
答 案: 4、已知直线l的斜率为1,l过抛物线C: 答 案:(I)C的焦点为 填空题 1、若tanα-cotα=1,则 答 案:4 解 析:由立方差公式得,tan3α-cot3α=(tana-cotα)(tan2α+tanαcota+cot2α)(tana-cotα)[(tanα-cotα)2+3tanαcotα]=4
2、y=cos22x的最大值是______,最小值______,周期T=______。
答 案:1;0; 解 析: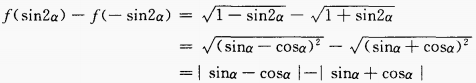
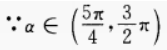 ∴sinα
∴sinα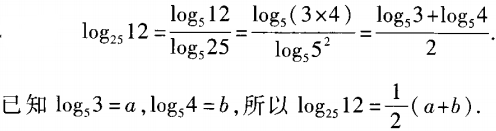
 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|. ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
 =______。
=______。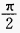
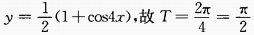 ,最大值为
,最大值为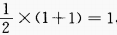 ,最小值为
,最小值为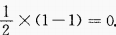
精彩评论