2025年成考高起点每日一练《数学(理)》4月19日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、已知x+x-1=2cos40°,则x4+x-4=().
- A:2cos20
- B:-2cos20°
- C:2sin80°
- D:-2sin80°
答 案:B
解 析:由已知得(x+x-1)2=(2 cos 40°)2,x2+2+x-2=4cos240°,x2+x-2=2(2 cos240°-1)=2cos 80°同样可得x4+x-4=2 cos 160°=-2 cos 20°
2、圆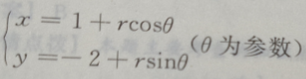 的圆心在()点上
的圆心在()点上
- A:(1,-2)
- B:(0,5)
- C:(5,5)
- D:(0,0)
答 案:A
解 析:因为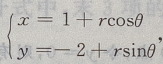 所以圆的圆心为O(1,-2)
所以圆的圆心为O(1,-2)
3、已知直线l:3x-2y-5=0,圆C: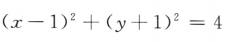 ,则C上到l的距离为1的点共有()
,则C上到l的距离为1的点共有()
- A:1个
- B:2个
- C:3个
- D:4个
答 案:D
解 析:由题可知圆的圆心为(1,-1),半径为2 ,圆心到直线的距离为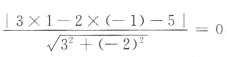 ,即直线过圆心,因此圆C上到直线的距离为1的点共有4个.
,即直线过圆心,因此圆C上到直线的距离为1的点共有4个.
4、设集合M={x∈R|x2=1},N={x∈R|x3=1},则M∩N=()。
- A:{1}
- B:{-1}
- C:{-1,1}
- D:

答 案:A
解 析:本题主要考查的知识点为集合的运算 由题意M={-1,1},N={1},所以M∩N={1}
主观题
1、已知数列 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。
答 案:

2、求将抛物线y=x2-2x-3平移到顶点与坐标原点重合时的函数解析式。
答 案:
3、如图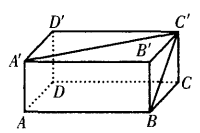 ,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
(2)A’B’和DD’的距离是多少?
答 案:(1)在长方体中BC和A’C’不在同一个平面内 所以BC和A’C’是异面直线 ∵在长方体中BC//B’C’ ∴∠A’C’B’是异面直线BC和A’C’所成的角
∵A’C’B’=45°
异面直线BC和A’C’所成的角是45°
(2)A’B’和DD’是异面直线
∵A’D’⊥A’B’ A’D’⊥DD’
∴A’D’的长即为异面直线A’B’和DD’的距离
∵A’D’=4
∴A’B’和DD’间的距离为4cm。
4、设函数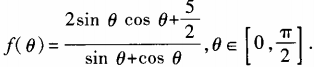 (1)求
(1)求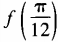 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
填空题
1、若平面向量a=(x,1),b=(1,-2),且a//b,则x=()
答 案: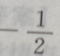
解 析:由于a//b,故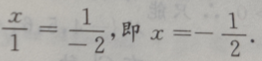
2、不等式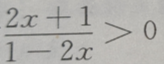 的解集为()
的解集为()
答 案: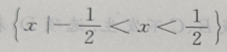
解 析:

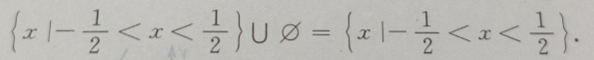
精彩评论