2025年成考专升本每日一练《高等数学一》4月20日专为备考2025年高等数学一考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、当x→0时,5x-sin5x是x的()。
- A:高阶无穷小量
- B:等价无穷小量
- C:同阶无穷小量,但不是等价无穷小量
- D:低阶无穷小量
答 案:A
解 析: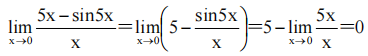 ,故5x-sin5x是x的高阶无穷小量.
,故5x-sin5x是x的高阶无穷小量.
2、设二元函数z=f(xy,x2+y2),且函数f(u,v)可微,则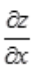 等于()。
等于()。
- A:y+2x
- B:
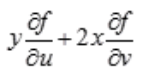
- C:
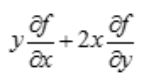
- D:
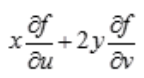
答 案:B
解 析: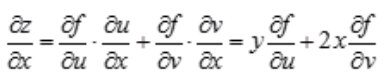 。
。
3、在空间直角坐标系中,方程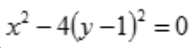 表示()。
表示()。
- A:两个平面
- B:双曲柱面
- C:椭圆柱面
- D:圆柱面
答 案:A
解 析:由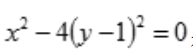 得
得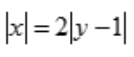 ,故为两个平面。
,故为两个平面。
主观题
1、试证:当x>0时,有不等式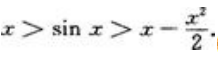
答 案:证:先证x>sinx(x>0)。设f(x)=x-sinx,则f(x)=1-cosx≥0(x>0),所以f(x)为单调递增函数,于是对x>0有f(x)>f(0)=0,即x-sinx>0,亦即x>sinx(x>0)。再证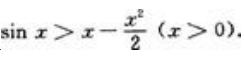
令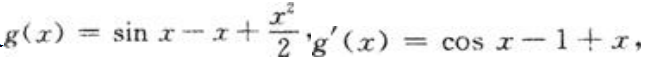
则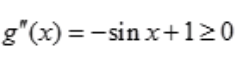 ,所以g'(x)单调递增,又g'(x)=0,可知g'(x)>g'(0)=0(x>0),那么有g(x)单调递增,又g(0)=0,可知g(x)>g(0)=0(x>0),所以
,所以g'(x)单调递增,又g'(x)=0,可知g'(x)>g'(0)=0(x>0),那么有g(x)单调递增,又g(0)=0,可知g(x)>g(0)=0(x>0),所以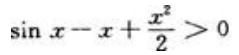 即
即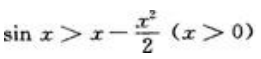
综上可得:当x>0时,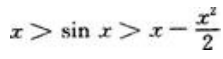 。
。
2、求函数y=xex的极小值点与极小值
答 案:解:方法一: 令y'=0,得x=-1。
令y'=0,得x=-1。
当x<-1时,y'<0;当x>-1时,y'>0。
故极小值点为x=-1,极小值为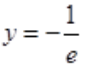 。
。
方法二:,
令y'=0,得x=-1,又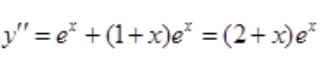 ,
, 。
。
故极小值点为x=-1,极小值为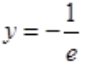 。
。
3、求微分方程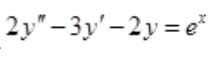 的通解。
的通解。
答 案:解: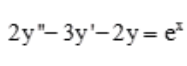 的特征值方程为
的特征值方程为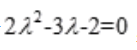 ,则
,则 ;故齐次微分方程的通解为
;故齐次微分方程的通解为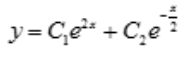 。由题意设原微分方程的特解为
。由题意设原微分方程的特解为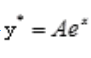 ,则有
,则有 ,得
,得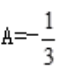 。即微分方程的通解为
。即微分方程的通解为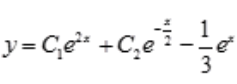 。
。
填空题
1、微分方程 的通解为y=_____。
的通解为y=_____。
答 案: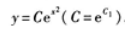
解 析:所给方程为可分离变量方程。 
2、微分方程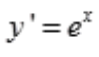 的通解是()。
的通解是()。
答 案:y=ex+C
解 析: ,分离变量,得dy=exdx,两边积分得y=ex+C,即为通解。
,分离变量,得dy=exdx,两边积分得y=ex+C,即为通解。
3、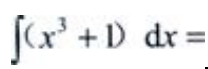 ()。
()。
答 案: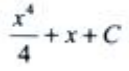
解 析:由不定积分性质,可得 。
。
简答题
1、求微分方程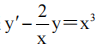 的通解.
的通解.
答 案:由题可知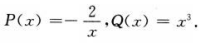 通解为
通解为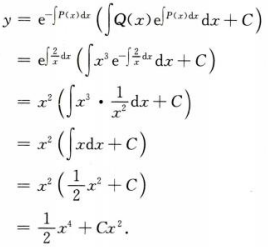
精彩评论