2025年成考高起点每日一练《数学(理)》4月21日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、函数y=x²—2x+6在区间（-∞，1）、（1，+∞）分别（）。

• A：单调增加、单调减少
• B：单调减少、单调增加
• C：单调增加、单调增加
• D：单调减少、单调减少

答 案：B

解 析：方法一：用配方法把y=x²-2x+6配成完全平方式。 y=x²-2x+6=（x-1）2+5，开口向上的抛物线顶点坐标为（1，5），可得出单调区间。 方法二：用导数判定。y’=2x-2=2（x-1）
当x<1时，y’<0，单调减少；当x>1时，y>0，单调增加。

2、设函数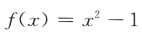，则f(x+1)=（）

• A：x²+2x+1
• B：x²+2x
• C：x²+1
• D：x²

答 案：B

解 析：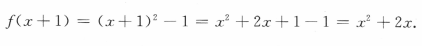

3、（ ）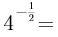

• A：-2
• B：
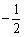
• C：
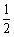
• D：2

答 案：C

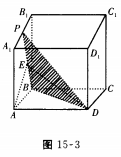
4、若P为正方体A1C中A1B1棱上的中点，则过P、B、D三点的平面与AA1B1B面所成的二面角的余弦值为（）。

• A：
• B：
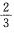
• C：
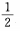
• D：

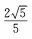
答 案：B

解 析：

主观题

1、某气象预报站天气预报的准确率为80%，计算（1）5次预报中恰有4次准确的概率； （2）5次中至少有次准确的概率.(计算结果保留两个有效数字).  

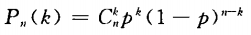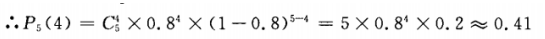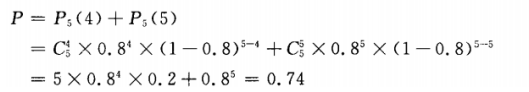答 案：  把每次预报看做一次试验，“预报结果准确”看成事件P（A）=0.8，本题就相当于在5次独立重复试验中求A恰好发生4次（或至少4次）的概率，此题属于独立重复试验，由公式来求解。 （1）n=5；p=0.8；k=4 即恰有4次准确的概率为0.41. (2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即 即至少有4次准确的概率为0.74。  

2、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得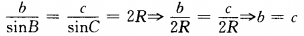

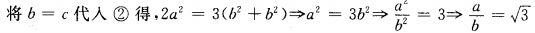
∴a：b=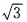：1
于是a：b：c=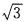：1：1。  

3、试证明下列各题
（1）
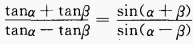
（2）

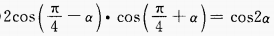
答 案：（1）化正切为正、余弦，通分即可得证。 （2）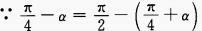

4、当自变量为何值时，函数y=2x³-3x²-12x+21有极值，其极值为多少？  

答 案：y'=6x²-6x-12=6（x-2）（x+1） 当x<-1或x>2时，y>0，当-1 故当x=-1时有极大值，其值为f（-1）=28 当x=2时有极小值，其值为f（2）=1

填空题

1、若tanα-cotα=1，则=______。

答 案：4

解 析：由立方差公式得,tan³α-cot³α=(tana-cotα)(tan²α+tanαcota+cot²α)(tana-cotα)[(tanα-cotα)²+3tanαcotα]=4  

2、曲线y=在点(1，1)处的切线方程是______。

答 案：2x+y-3=0

解 析：本题主要考查的知识点为切线方程 由题意，该切线斜率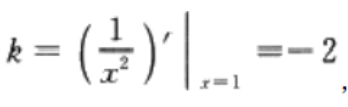， 又过点(1，1)，所以切线方程为y-1=-2(x-1)