2025年成考专升本每日一练《高等数学二》4月22日专为备考2025年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、设事件A、B互不相容,且P(A)=0.4,P(B)=0.5,则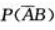 等于( ).
等于( ).
- A:0.9
- B:0.5
- C:0.4
- D:0.1
答 案:B
解 析:A、B互不相容,则两者不同时发生,A∩B为空集;故
2、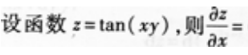 ()。
()。
- A:
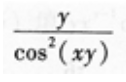
- B:
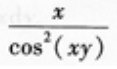
- C:
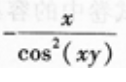
- D:
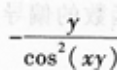
答 案:A
主观题
1、设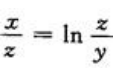 ,求
,求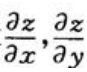 .
.
答 案:解:将方程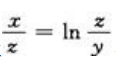 写成
写成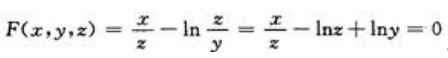 .因为
.因为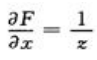 ,
,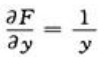 ,
,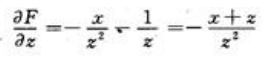 ,所以
,所以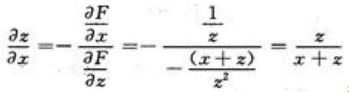 ,
,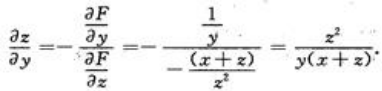
2、求函数f(x)=x3-3x2-9x+2的单调区间和极值.
答 案:解:函数f(x)的定义域为(-∞,+∞).f'(x)=3x2-6x-9=3(x+1)(x-3),令f'(x)=0,得驻点x1=-1,x2=3.
因此f(x)的单调增区间是(-∞,-1),(3,+∞);单调减区间是(-1,3).
f(x)的极小值为f(3)=-25,极大值f(-1)=7.
填空题
1、若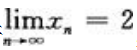 ,则
,则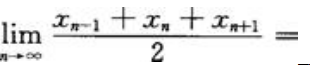 ().
().
答 案:3
解 析:因为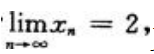 又因为数列有无极限和其极限值是多少与数列中含有限项的个数无关,所以
又因为数列有无极限和其极限值是多少与数列中含有限项的个数无关,所以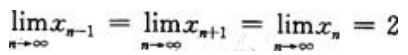 ,则原式=3.
,则原式=3.
2、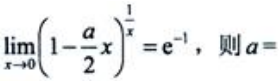 ().
().
答 案:2
解 析: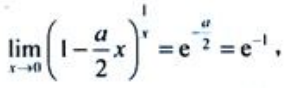 所以a=2.
所以a=2.
简答题
1、从一批有10件正品及2件次品的产品中,不放回地一件一件地抽取产品,设每个产品被抽到的可能性相同,求直到取出正品为止所需抽取的次数X的概率分布。
答 案:由题意,X的所有可能的取值为1,2,3, X=1,即第一次就取到正品,P{X=1}=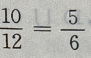 X=2,即第一次取到次品且第二次取到正品,P{X=2}=
X=2,即第一次取到次品且第二次取到正品,P{X=2}=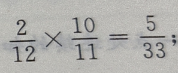 同理,P{X=3}=
同理,P{X=3}=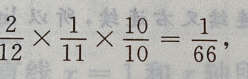 故X的概率分布如下
故X的概率分布如下
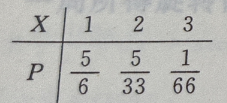
2、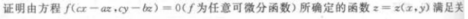

答 案:这是由抽象函数的复合函数所确定的隐函数的求偏导,应用复合函数求偏导及隐函数求 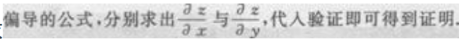

精彩评论